Loading... ## 问题描述 在二维平面上 n 个点中找出距离最小的两个点。 ## 暴力法 将所有点之间的距离遍历一遍。n 个点就需要遍历 $C_n^2$ 次。 **优点:** - 代码简单,易于实现。 - 数据量较小的时候较为实用 **缺点:** - 数据量较大的时候耗时指数级增长 **伪代码:** ```c minDistance = INF for first in len(points) for second in first to len(points) curDistance = calcDistance(points[first], points[second]) if curDistance < minDistance minDistance = curDistance savePoint(points[first], points[second]) ``` **时间复杂度:** 通过伪代码可以看到,主要循环部分为计算两点间距离,故 $ T(n) = C_n^2 \cdot 2 = n(n - 1) $ ,因此 $ O(n) = n^2 $ **空间复杂度:** 暴力法无需申请额外的空间,故空间复杂度为 $ O(1) $ ## 分治法 暴力法显然时间复杂度过高,数据量较大的时候就不适合了。所以我们使用分治法进行优化。 **首先简单介绍一下分治法:** 分治法字面上的解释是“分而治之”,就是将复杂的问题分解成多个简单的问题进行求解。 **分治法适用的场景:** - 该问题的**规模**缩小到一定的程度就可以容易地解决 - 该问题可以分解为若干个规模较小的相同问题,即该问题具有**最优子结构性质** - 利用该问题分解出的子问题的解可以合并为该问题的解 - 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含**公共的子问题**。 **分治法的基本步骤:** 分治算法可以分三步走:分解 -> 解决 -> 合并 1. 分解原问题为结构相同的子问题。 2. 分解到某个容易求解的边界之后,进行递归求解。 3. 将子问题的解合并成原问题的解。 ### **问题分析:** 首先我们知道,一个点和两个点的时候求解很简单,那么我们能不能想办法将原问题分解为一个点或者两个点的情况。 那么我们将原始的点对分解成两部分,那么最近的点对就有三种情况:**全在左边,全在右边,两边各一个** 。所以最终解就是三种情况中的最小值。 左右两边和原问题是一模一样的,所以直接递归求解即可。将左,右部分最小点对的距离记为 $ \delta_L, \delta_R $ 。 下面着重讨论两边各一个点的情况。最简单的方法就是使用蛮力法,直接将左边所有的点挨个和右边的点算距离,然后找出最小值。但这样的话总体看起来和暴力法差不多了,所以我们需要进一步优化: 选取 $\delta_L, \delta_R$ 中较小的值,记为 $ \delta $ 。然后在分界线旁画出宽度为 $2\delta$ 的长带(如下图),只有在这条长带内的点才可能小于 $\delta$ 。 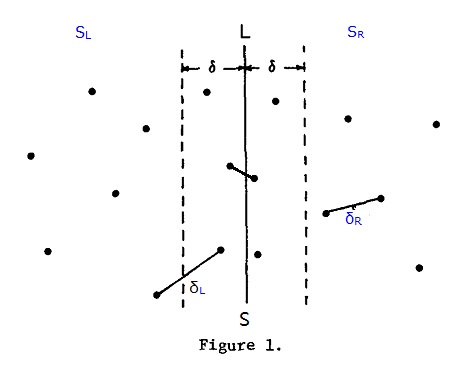 接着按照点的 y 值排序。此时对于左边的点来说,只要判断右边与该点 y 值最近的六个的点即可。这个结论可以用**反证法**或**[鸽舍原理](https://zh.wikipedia.org/wiki/鴿巢原理)**进行证明: **反证法证明:** 若右边的矩阵中有第七个点 $q$ 与左边的点 $p$ 的距离小于 $\delta$ ,则 $q$ 必定与矩形的一个顶点距离小于 $\delta$ (如下图)。这与 $\delta$ 是左右两边的最小距离相矛盾,所以最多只需要判断 6 个点。 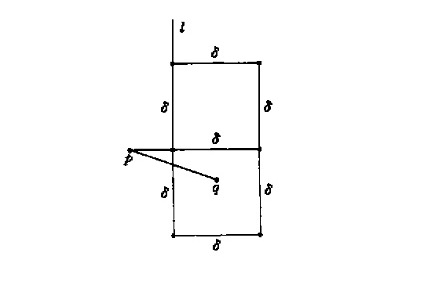 ### 伪代码: ```c def closestPoints(points) len = points.length sort(points, points + len, x) // sorted by x _closestPoints(points, len) def _closestPoints(points, len) if len < 2 return Infinity else if len == 2 savePoints // update closest point pair return calcDistance(points[0], points[1]) else left = _closestPoints(points.leftHalf, len / 2) right = _closestPoints(points.rightHalf, len / 2) minDistance = min(left, right) savePoints mid = points.mid // get the dividing line tmp = points[abs(x - mid) < minDistance] for point in tmp find the nearest six points judge and update minDistance save closest point pair ``` ### 算法分析 **排序过程:** 使用快排进行升序排序,复杂度为 $O(nlogn)$ **分治过程:** 对于每个左边的点,都要和 6 个右边的点进行比较,故时间复杂度计算公式为: $$ T(n) = \begin{cases} 1 & \text{$n$ = 1 or $n$ = 2} \\ 2T(\frac{n}{2}) + \frac{n}{2} \times 6 & \text{$n$ > 2} \end{cases} $$ 带入主定理即可解出时间复杂度。 综上:分治法的时间复杂度为 $ O(3nlogn) $ ## 代码实现: **蛮力法:** <div class="hideContent">该部分仅登录用户可见</div> **分治法:** <div class="hideContent">该部分仅登录用户可见</div> 最后修改:2020 年 04 月 12 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏