Loading... ## 树 ### 定义及基本术语 树是 $n (n \geq 0)$ 个节点的有限集合,$n = 0$ 时称为空树。在任意一颗非空树中应该满足: 1. 有且仅有一个特定的称为**根**的节点。 2. 当 $n \geq 1$ 时,其余节点可分为 $m (m > 0)$ 个**互不相交的有限集合**,其中每个集合本身又是一棵树,且称为根节点的**子树**。 > 树是一种递归定义的数据结构。 树的一些特点: - 非空树有且仅有一个根节点。 - 没有后继的节点称为叶子节点。 - 有后继的节点称为分支节点。 - 除了根节点外任何一个节点都有且仅有一个前驱。 - 每个节点可以由零个或多个后继。 节点之间的关系: - 祖先节点 - 子孙节点 - 双亲节点 (父节点) - 孩子节点 (子节点) - 兄弟节点 - 堂兄弟节点:在树中同一层但不是同一个父节点的节点。(不常用) 树的属性: - 节点的层次 (深度) :从上往下数,默认从 1 开始。 - 节点的高度:从下往上数。 - 树的深度:总共多少层。 - **节点的度**:有几个孩子 (分支) 。 - **树的度**:各节点度的最大值。 ### 有序树 && 无序树 有序树:逻辑上看,树中节点的各子树从左到右是有次序的,不可互换。 无序树:逻辑上看,树中节点的各子树从左到右是无次序的,可以互换。 ### 森林 森林是 $m (m \geq 0)$ 棵互不相交的树的集合。当 $m = 0$ 时,该森林为空森林。 ### 考点 1. 节点数 = 总度数 + 1 。 节点的度表示节点有几个子节点,根节点没有父节点,所以需要加一。 2. 度为 $m$ 的树和 $m$ 叉树的区别。 | 度为$m$ 的树 | $m$ 叉树 | | --------------------------------------- | --------------------------------------- | | 任意节点的度$ \leq m$ (最多 $m$ 个孩子) | 任意节点的度$ \leq m$ (最多 $m$ 个孩子) | | 至少有一个节点的度为$m$ (有 $m$ 个孩子) | 允许所有节点的度$\leq m$ | | 一定是非空树,至少有$m + 1$ 个节点 | 可以是空树 | 3. 度为 $m$ 的树第 $i$ 层最多有 $m^{i - 1}$ 个节点。($i \geq 1$) 。 4. 高度为 $h$ 的 $m$ 叉树至多有 $\frac{m^h - 1}{m - 1}$ 个节点。 5. 高度为 $h$ 的 $m$ 叉树至少有 $h$ 个节点,高度为 $h$ ,度为 $m$ 的树则至少有 $h + m + 1$ 个节点。 6. 具有 $n$ 个节点的 $m$ 叉树的最小高度为 $\lceil log_m(n(m - 1) + 1) \rceil$ 。 ## 二叉树 ### 定义及基本术语 二叉树是 $n (n \geq 0)$ 个节点的有限集合,其满足以下条件: 1. $n = 0$ 时,为空二叉树。 2. $n \neq 0$ 时,由一个**根节点**和两个互不相交的被称为根的左子树和右子树组成,且左子树和右子树又分别为一棵二叉树。 特点: - 每个节点至多只有两颗子树。 - 左右子树不可颠倒 ( 二叉树是有序树) 。 ### 一些特殊的二叉树 - 满二叉树:一棵高度为 $h$ ,且含有 $2^h - 1$ 个节点的二叉树。 - 只有最后一层有叶子节点。 - 不存在度为 1 的节点。 - 按层序从 1 开始编号,节点 $i$ 的左孩子为 $2i$ ,右孩子为 $2i + 1$ ,父节点为 $\lfloor i / 2 \rfloor$ 。 (如果存在的话) - 完全二叉树:当且仅当其每个节点都与高度为 $h$ 的满二叉树中编号为 $1$ ~ $n$ 的节点一一对应时,称为完全二叉树。 - 只有最后两层可能有叶子节点。 - 最多只有一个度为 1 的节点。 - 按层序从 1 开始编号,节点 $i$ 的左孩子为 $2i$ ,右孩子为 $2i + 1$ ,父节点为 $\lfloor i / 2 \rfloor$ 。 (如果存在的话) - $i \leq \lfloor n / 2 \rfloor$ 的为分支节点, $i \geq \lfloor n / 2 \rfloor$ 的为叶子节点。 - 二叉排序树:一颗二叉树为空二叉树,或者是满足以下性质的二叉树: - 左子树上所有节点的关键字均小于根节点的关键字; - 右子树上所有节点的关键字均大于根节点的关键字; - 左子树和右子树又各是一棵二叉排序树。 - 平衡二叉树:树上任意节点的左子树和右子树的**深度之差不超过 1** 。 > 平衡二叉树拥有更高的搜索效率。 > ### 二叉树的存储方式 #### 顺序存储 定义一个长度为 `MAX_SIZE` 的数组 t ,按照从上至下,从左至右的顺序依次存储完全二叉树中的各个节点。 > 一定要把二叉树的节点编号与完全二叉树对应起来。 ```c++ struct TreeNode { ElemType value; bool isEmpty }; TreeNode t[MAX_SIZE]; ``` 常考的基本操作: - $i$ 的左孩子: $2i$ - $i$ 的右孩子:$2i + 1$ - $i$ 的父节点:$\lfloor i / 2 \rfloor$ - $i$ 所在的层次:$\lceil log_2(n + 1) \rceil$ 或 $\lfloor log_2 n \rfloor + 1$ 若完全二叉树中共有 $n$ 个节点,则: - 判断 $i$ 是否有左孩子:$2i \leq n$ ? - 判断 $i$ 是否有右孩子:$2i + 1 \leq n$ ? - 判断 $i$ 是否为叶子节点:$i > \lfloor n / 2 \rfloor$ ? > 如果不是完全二叉树,直接判断对应位置是否为空即可。 二叉树的顺序存储结构只适合存储完全二叉树,存储非完全二叉树会有很多空间浪费。 #### 二叉树的链式存储 ```c++ typedef struct BiTNode { ElemType data; struct BiTNode *lchild, *rchild; } BiTNode, *BiTree; ``` > $n$ 个节点的二叉链表共有 $n + 1$ 个空链域,可以用于构造线索二叉树 (后面会提到) 上述方式可以很快找到左右孩子,但找父节点只能从根节点开始遍历。如果需要快速找到父节点可以增加一个指向父节点的指针,称为三叉链表: ```c++ typedef struct BiTNode { ElemType data; struct BiTNode *lchild, *rchild; struct BiTNode *parent; } BiTNode, *BiTree; ``` ### 二叉树的遍历 遍历:按照某种次序把所有的节点都访问一遍。 二叉树的递归特性: - 要么是个空二叉树 - 要么就是由 "根节点 + 左子树 + 右子树" 组成的二叉树。 #### 先序遍历 按照 `根 -> 左 -> 右 (NLR)` 顺序遍历二叉树。 ```c++ void PreOrder (BiTree T) { if (T == NULL) return; visit(T); // 访问根节点 PreOrder(T->lchild); PreOrder(T->rchild); } ``` #### 中序遍历 按照 `左 -> 根 -> 右 (LNR)` 顺序遍历二叉树。 ```c++ void InOrder (BiTree T) { if (T == NULL) return; InOrder(T->lchild); visit(T); // 访问根节点 InOrder(T->rchild); } ``` #### 后序遍历 按照 `左 -> 右 -> 根 (LRN)` 顺序遍历二叉树。 ```c++ void PostOrder (BiTree T) { if (T == NULL) return; PostOrder(T->rchild); PostOrder(T->lchild); visit(T); // 访问根节点 } ``` #### 层序遍历 算法流程: 1. 初始化一个辅助队列 2. 根节点入队 3. 若队列非空,则队头出队,访问该节点,并将其左右孩子入队(如果存在的话) 4. 重复 3 直到队列非空 #### 由遍历序列构造二叉树 根据**前序遍历**和**中序遍历**可以构造出独一无二的二叉树。前序遍历的第一个一定是根节点,然后根据中序遍历可以确定左子树和右子树,再用同样的方法递归判断左右子树即可。 根据**后序遍历**和**中序遍历**也可以构造出独一无二的二叉树,后序遍历最后一个一定是根节点,其余和上述方法一致。 已知**层序**和**中序遍历**也可以构造出二叉树,因为层序遍历第一个元素是根节点,接下来两个元素分别是左子树和右子树的根,然后再根据中序序列找到左右子树,接着递归判断左右子树即可。 ### 考点 **二叉树的常考性质**: 1. 设非空二叉树中度为 0,1,2的节点数分别为 $n_0, n_1, n2$ ,则 $n_0 = n_2 + 1$ 。(叶子节点比二分支节点数多一个) 证明:假设树中节点总数为 $n$ ,则有 $n = n_0 + n_1 + n_2$ 。又知 $n = n_1 + 2n_2 + 1$ (节点数与度的关系) ,所以有 $n_0 = n_2 + 1$ 。 2. 二叉树的第 $i$ 层至多有 $2^{i - 1}$ 个节点。($i \geq 1$) 3. 高度为 $h$ 的二叉树至多有 $2^h - 1$ 个节点。 **完全二叉树的常考性质**: 1. 具有 $n$ 个 ($n > 0$) 节点的完全二叉树的高度为 $\lceil log_2(n + 1) \rceil$ 或 $\lfloor log_2n \rfloor + 1$ 。 2. 对于完全二叉树,可以由节点数 $n$ 推出度为 $0, 1, 2$ 的节点个数 $n_0, n_1, n_2$ 。 - 完全二叉树最多只有一个度为 1 的节点; - $n_0 = n_2 + 1$ 。 ## 线索二叉树 ### 定义 > 以下以中序线索二叉树为例,前后序都是类似的。 前面提到过 $n$ 个节点的二叉链表共有 $n + 1$ 个空链域,线索二叉树就是利用这些空链域,记录下每个节点的前驱和后继。这些指向前驱和后继的指针就称为**线索**。 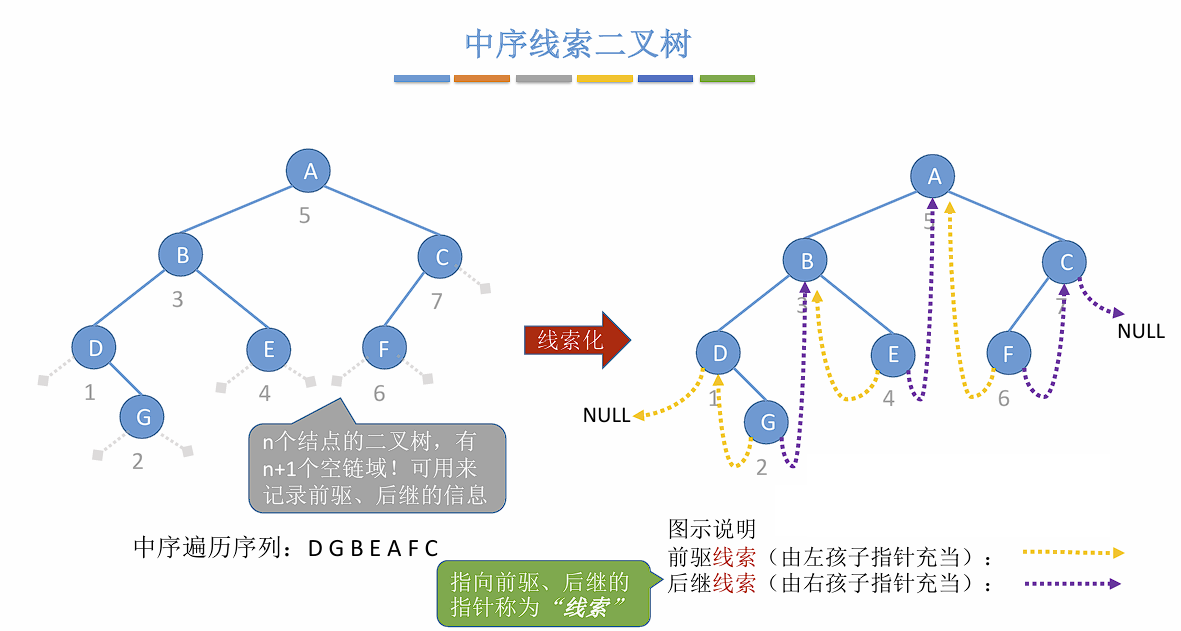 **作用**:方便从一个指定的节点出发,找到其前驱和后继。同时也可以从指定节点开始遍历子树。 ### 存储结构 ```c++ typedef struct BiTNode { ElemType data; struct BiTNode *lchild, *rchild; int ltag, rtag; // 左右线索标志 } BiTNode, *BiTree; ``` 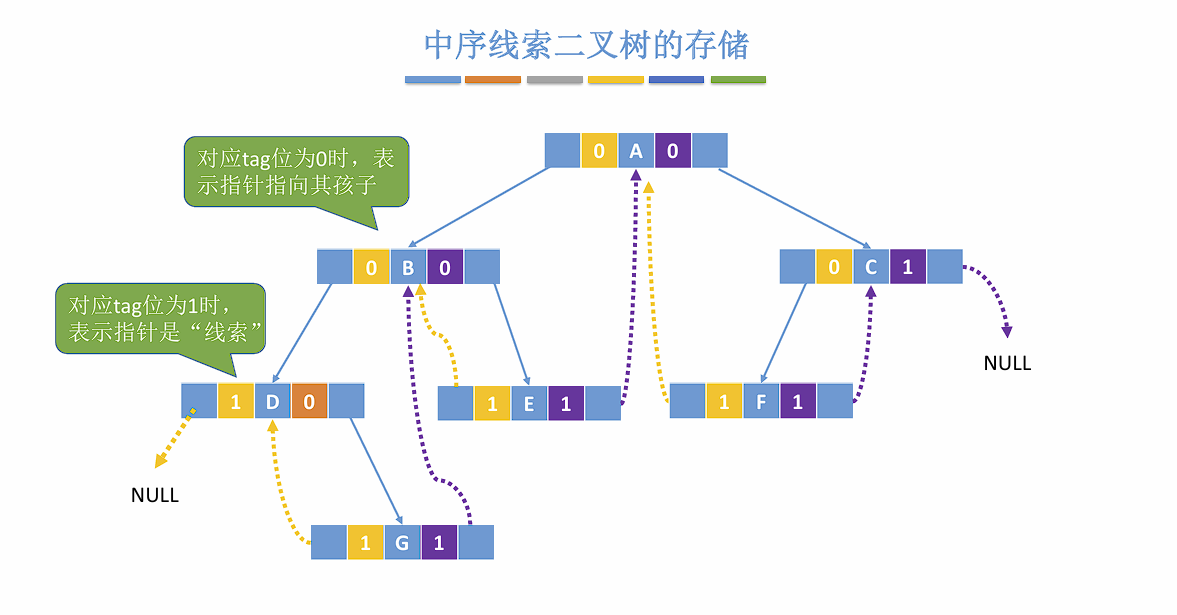 ### 二叉树的线索化 以中序线索化为例: ```c++ void InThread (ThreadTree p, ThreadTree &pre) { if (p == NULL) return; InThread(p->lchild, pre); if (p->lchild == NULL) { p->lchild = pre; p->ltag = 1; } if (pre != NULL && pre->rchild == NULL) { pre->rchild = p; pre->rtag = 1; } pre = p; InThread(p->rchild, pre); } // 中序线索化二叉树 void CreateInThread(ThreadTree T) { if (T == NULL) return; ThreadTree pre = NULL; InThread(T, pre); pre->rchild = NULL; pre->rtag = 1; } ``` 先序线索化中可能存在环路,需要判断下一个节点是否为线索。 ```c++ void PreThread(ThreadTree p, ThreadTree &pre) { if (p == NULL) return; if (p->lchild == NULL) { p->lchild = pre; p->ltag = 1; } if (pre != NULL && pre->rchild == NULL) { pre->rchild = p; pre->rtag = 1; } pre = p; // 此处需要特殊判断一下防止环路 if (p->ltag == 0) PreThread(p->lchild, pre); PreThread(p->rchild, pre) } ``` ### 线索二叉树寻找前驱后继  如果使用三叉链表,则可以找到先序的前驱和后序的后继。 ### 考点 1. 手算画出线索二叉树 - 确定线索二叉树的类型,先序,中序还是后序。 - 按照对应的遍历规则,确定各个节点的访问顺序,并写上编号。 - 将 $n + 1$ 个空链域连上前驱和后继。 2. 线索化的易错点 - 最后一个节点的 `rchild` 和 `rtag` 需要处理; - 先序线索化中注意处理环路。 ## 树的存储结构 只依靠数组下标,无法反映节点之间的逻辑关系,因为每个节点下的子树个数是不确定的。 ### 双亲表示法 一种思路是可以用数组顺序存储各个节点,每个节点中保存数据元素以及指向父节点的 "指针" 。(类似于静态链表) ```c++ typedef struct { ElemType data; int parent; // 父节点位置 } PTNode; typedef struct { PTNode nodes[MAX_TREE_SIZE]; int n; } PTree; ``` 双亲表示法也可以用来存储森林: 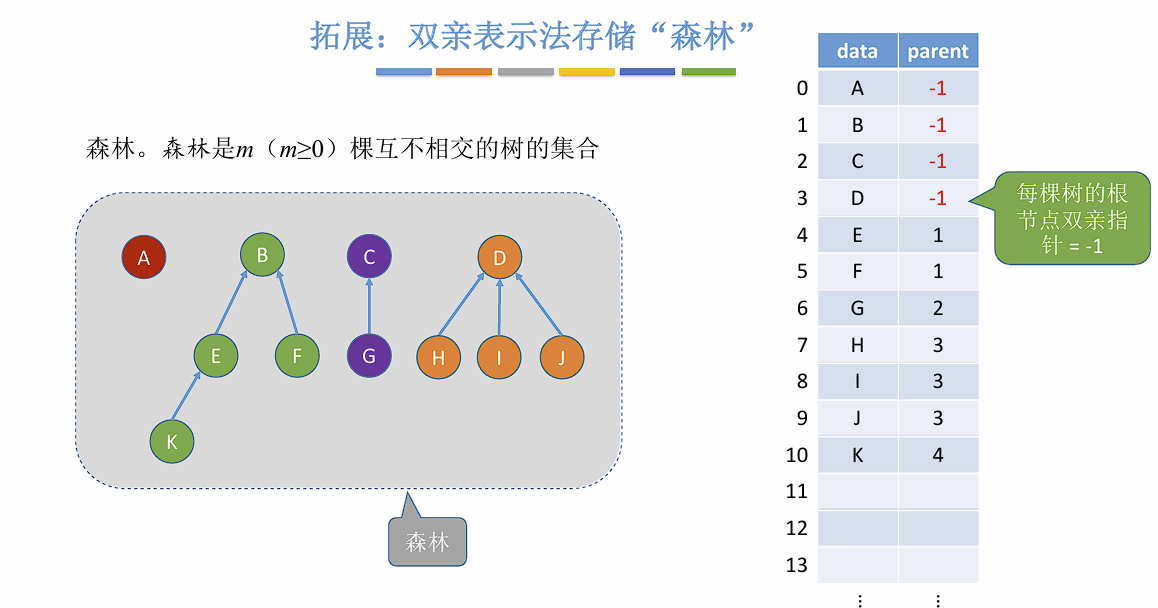 - 优点:找父节点方便。 - 缺点:找孩子节点不方便,需要遍历所有节点。 适用于找父节点多,子节点少的场景,如并查集。 ### 孩子表示法 顺序存储和链式存储的结合。用数组顺序存储各个节点,每个节点中保存**数据元素**以及**子链表头指针**。 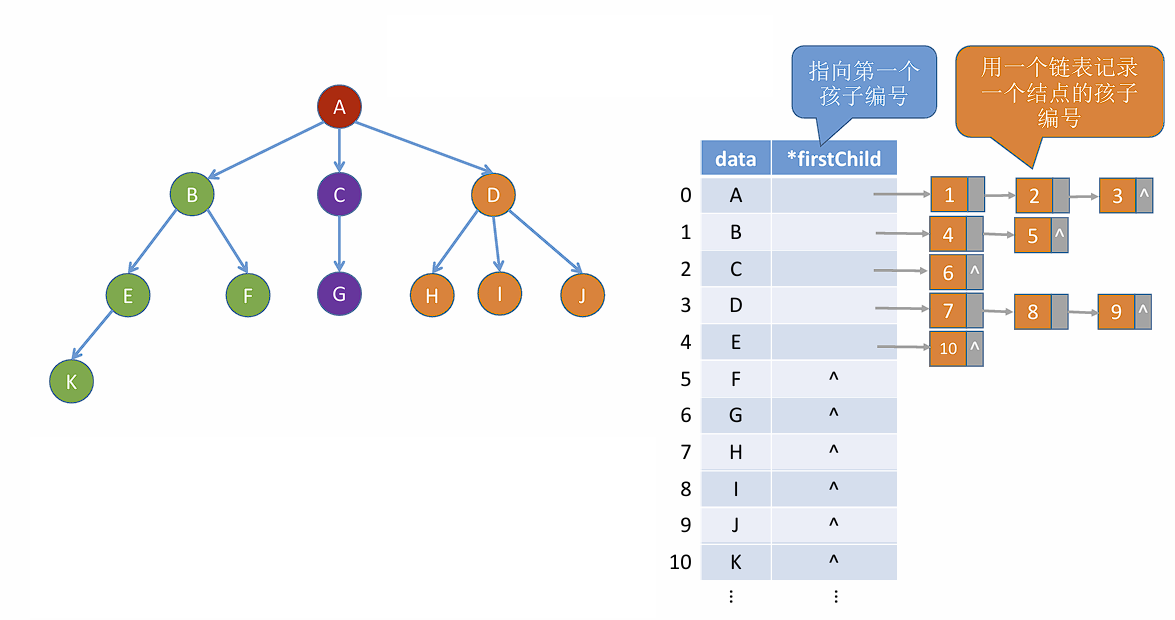 ```c++ struct CTNode { int child; // 子节点在数组中的位置 struct CTNode *next; }; typedef struct { ElemType data; struct CTNode *firstChild; } CTBox; typedef struct { CTBox nodex[MAX_TREE_SIZE]; int n, root; // 节点数和根的位置 } CTree; ``` 这种方式也可以用于存储森林,需要记录多个根的位置。 - 优点:找子节点方便。 - 缺点:找父节点不方便,只能遍历每个链表。 适用于找子节点多,找父节点少的应用场景,如:服务流程树。 ### 孩子兄弟表示法 与二叉树类似,采用二叉链表实现。每个节点中保存数据元素和两个指针,一个指针指向该节点的第一个子节点,另一个指针指向该节点右边的第一个兄弟节点。  该方法同样可以存储森林:  ## 树,森林,二叉树之间的转换 ### 树 -> 二叉树 先在二叉树中初始化根节点,然后按照树的层序依次处理每个节点。节点的处理方法参考上面的孩子兄弟表示法。 ### 森林 -> 二叉树 同样参考孩子兄弟表示法。 ### 二叉树 -> 树 先画出树的根节点,然后按树的层序恢复每个节点的子节点。 在二叉树下,如果当前处理的节点有左孩子,就把左节点和所有递归的的右孩子拆下来,按顺序挂在当前节点下方。 ### 二叉树 -> 森林 先把二叉树的根节点和其递归的右节点拆下来,作为多棵树的根节点。接着按森林的层级恢复每个节点的孩子。恢复方法参考二叉树 -> 树。 ## 树和森林的遍历 ### 树的遍历 - 先根遍历:若树非空,先访问根节点,再依次对每棵子树进行先根遍历。 树的先根遍历序列与这棵树对应二叉树的先序遍历序列相同。 - 后根遍历:若树非空,先依次对每棵子树进行后根遍历,最后再访问根节点。 树的后根遍历序列和这棵树对应二叉树的中序遍历序列相同。 - 层次遍历:使用队列实现,和二叉树的层次遍历相同。 ### 森林的遍历 - 先序遍历:对每棵树的每棵树进行先根遍历。 森林的先序遍历与这个森林对应二叉树的先序遍历序列相同。 - 中序遍历:对森林中的每棵树进行后根遍历 森林的后序遍历与这个森林对应二叉树的中序遍历序列相同。  ## 霍夫曼树 ### 定义 一些名词的含义: - 节点的**权**:有某种现实含义的数值,如表示节点的重要性。 - 节点的**带权路径长度**:从树的根到该节点的路径长度 (经过的边数) 与该节点上权值的乘积。 - 树的**带权路径长度**:树中所有叶节点的带权路径长度之和 (WPL, Weighted Path Length) 霍夫曼树的定义:在含有 $n$ 个带权叶节点的二叉树中,其中**带权路径长度最小**的**二叉树**称为**霍夫曼树**,又称**最优二叉树**。 ### 构造 给定 $n$ 个权值分别为 $w_1, w_2, ... , w_n$ 的节点,构造霍夫曼树的算法描述如下: 1. 将这 $n$ 个节点分别作为 $n$ 棵仅含一个节点的二叉树,构成森林 $F$ 。 2. 构造一个新节点,从 $F$ 中取两棵根节点权值最小的树作为新节点的左右子树,并将新节点的权值设置为左右子树上根节点的权值之和。 3. 从 $F$ 中删除刚才选出的两棵树,同时将新的数加入到 $F$ 中。 4. 重复步骤 2 和 3 ,直到 $F$ 中只剩下一棵树为止。 霍夫曼树具有以下特点: - 每个初始节点最终都会成为叶子节点,且权值越小的节点到根节点的路径越长。 - 霍夫曼树的节点总数为 $2n - 1$ 。 - 霍夫曼树中不存在度为 1 的节点。 - 霍夫曼树并不唯一,但 WPL 必然相同且最优。 ### 霍夫曼编码 固定长度编码:每个字符用相同长度的二进制位表示,比如 ASCII 码。 可变长度编码:允许对不同字符用不等长的二进制位表示。若没有一个编码是另一个编码的前缀,则称这样的编码为**前缀编码**。 霍夫曼编码是一种前缀编码,由霍夫曼树得到。字符集中每个字符作为一个叶子节点,各个字符出现的频度作为权值,根据前面的构造方法构造出霍夫曼树,即可得到霍夫曼编码。该编码可以用于数据压缩。 #### 多元霍夫曼编码 多元树霍夫曼编码算法使用字母集 $\{0, 1, ... , n − 1\}$ ,来构建一棵 $n$ 元树。霍夫曼在他的原始论文中考虑了这种方法。这与二进制($n=2$)算法仅有的差别,就是它每次把 $n$ 个最低权的符号合并,而不仅是两个最低权的符号。 倘若 $n \geq 2$ , 则并非所有源字集都可以正确地形成用于霍夫曼编码的多元树。在这些情况下,**必须添加额外的零概率占位符**。这是因为该树必须为满的 $n$ 叉树,所以每次合并会令符号数恰好减少 $n -1$ , 故这样的 $n$ 叉树存在**当且仅当源字的数量模 $n -1$ 余 1** 。 对于二进制编码,任何大小的集合都可以形成这样的二叉树,因为 $n -1 = 1$ 。 ## 并查集 > 可以参考 https://leetcode.cn/circle/discuss/qmjuMW/ ### 定义 并查集的逻辑结构为集合。集合中的元素有两种关系:在同一个集合内或不在同一个集合内。 并查集 (不相交集) 是一种描述不相交集合的数据结构,即若一个问题涉及多个元素,它们可划归到不同集合,同属一个集合内的元素等价(即可用任意一个元素作为代表),不同集合内的元素不等价。 ### 基本操作 并查集是集合的一种具体实现,只进行**并**和**查**两种基本操作。 - 查 (Find) :确定一个指定元素所属的集合。 - 并 (Union) :将两个不相交的集合合并为一个。 > 并查集之前用 C++ 写过,所以这里给出 C++ 的实现代码。 ```c++ class UnionFind { private: std::vector<int> parent; public: explicit UnionFind(const int &n) { parent.resize(n, -1); } void unite(const int &x, const int &y) { int xRoot = find(x), yRoot = find(y); if (xRoot == yRoot) // 在同一个集合内不需要合并 return; parent[yRoot] = xRoot; } int find(const int &x) { return parent[x] < 0 ? x : find(parent[x]); } }; ``` - 最坏情况下所有节点都串成一条链表,此时 `find` 的时间复杂度为 $O(n)$ ; - 除去 `find` 操作的时间情况下, `union` 时间复杂度为 $O(1)$ 。 ### 优化 #### 启发式合并 合并时,选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。我们可以将节点较少或深度较小的树连到另一棵,以免发生退化。 这里设定节点的编号一定大于 0 ,所以可以使用负数来记录树的长度: ```c++ class UnionFind { private: std::vector<int> parent; public: explicit UnionFind(const int &n) { parent.resize(n); } void unite(const int &x, const int &y) { int xRoot = find(x), yRoot = find(y); if (xRoot == yRoot) return; // 将较矮的树合并到较高的树上。 // 如果两棵树高度不一致,则合并后树高不变; // 如果两棵树高度一致,则合并后需要将树高加一,即根节点 parent 值减一。 if (parent[xRoot] < parent[yRoot]) { parent[yRoot] = xRoot; } else if (parent[xRoot] > parent[yRoot]) { parent[xRoot] = yRoot; } else { parent[yRoot] = xRoot; parent[xRoot] -= 1; } } int find(const int &x) { return parent[x] < 0 ? x : find(parent[x]); } }; ``` 该方法构造的树高不超过 $\lfloor log_2n \rfloor + 1$ ,因此`union` 的最坏时间复杂度降低至 $O(logn)$ 。 #### 路径压缩 查询过程中经过的每个元素都属于该集合,我们可以将其直接连到根节点以加快后续查询。 ```c++ class UnionFind { private: std::vector<int> parent; public: explicit UnionFind(const int &n) { parent.resize(n); } void unite(const int &x, const int &y) { int xRoot = find(x), yRoot = find(y); if (xRoot == yRoot) return; if (parent[xRoot] < parent[yRoot]) { parent[yRoot] = xRoot; } else if (parent[xRoot] > parent[yRoot]) { parent[xRoot] = yRoot; } else { parent[yRoot] = xRoot; parent[xRoot] -= 1; } } int find(const int &x) { // 查找根节点的同时把该节点直接接在根节点上 return parent[x] < 0 ? x : parent[x] = find(parent[x]); } }; ``` ### 复杂度 #### 时间复杂度 同时使用路径压缩和启发式合并之后,并查集的每个操作平均时间仅为 $O(\alpha(n))$ ,其中 $\alpha(n)$ 为阿克曼函数的反函数,其增长极其缓慢,也就是说其单次操作的平均运行时间可以认为是一个很小的常数。 [Ackermann 函数](https://en.wikipedia.org/wiki/Ackermann_function) $A(m, n)$ 的定义是这样的: $$ \begin{equation} A(m, n) = \begin{cases} n + 1 &\mbox{if m = 0} \\ A(m - 1, 1) &\mbox{if m > 0 and n = 0} \\ A(m - 1, A(m, n - 1)) &\mbox{otherwise} \\ \end{cases} \end{equation} $$ 而反 `Ackermann` 函数 $\alpha (n)$ 的定义是阿克曼函数的反函数,即为最大的整数 $m$ 使得 $A(m, m) \leq n$ 。时间复杂度的证明可以参考[这个页面中的证明](https://oi-wiki.org/ds/dsu-complexity/)。 #### 空间复杂度 显然为 $O(n)$ 。 最后修改:2024 年 11 月 19 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏