Loading... 在 IEEE754 标准中,float(单精确度浮点数) 型数据由 符号位(sign),指数偏移值(exponent bias),分数值(fraction)组成。那么如果分数值精度不够了,就会涉及到 float 数据的舍入问题。 先来个小例子看看: ```c #include <stdio.h> int main() { float a = 1234567890; double b = 1234567890; printf("%f\n%f\n", a, b); return 0; } ``` 上面代码的输出结果如下: ``` 1234567936.000000 1234567890.000000 ``` 可以看到 double 类型和原数一样,而 float 型数据进行了舍入操作。下面来看看 float 的舍入规则。 IEEE标准列出4种不同的方法: - **舍入到最接近**:舍入到最接近,在一样接近的情况下偶数优先(Ties To Even,这是默认的舍入方式):会将结果舍入为最接近且可以表示的值,但是当存在两个数一样接近的时候,则取其中的偶数(在二进制中是以0结尾的)。 - **朝 $ + \infty $ 方向舍入**:会将结果朝正无限大的方向舍入。 - **朝 $ - \infty $ 方向舍入**:会将结果朝负无限大的方向舍入。 - **朝0方向舍入**:会将结果朝0的方向舍入。 上面的例子就是用的第一种舍入方法,我画了个流程图方便理解: 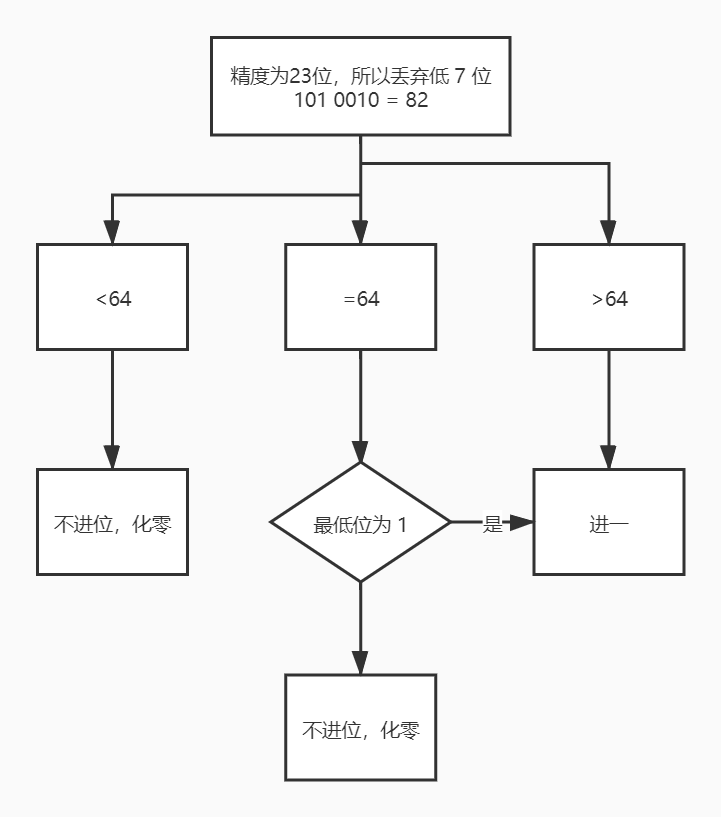 最后修改:2020 年 04 月 08 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏