Loading... > ***解析几何的巅峰 > 是 向量 > 那无关过程的狂妄与简洁 > 映射着大自然无与伦比的美*** > ——(出处在最下方参考资料中) ##题目: ```markdown ###题目描述 每个线段是用平面上的两个点来描述,用结构体实现对于任意输入的2个线段,判断其是否相交。 提示:两点(x1,y1), (x2,y2) 间直线斜率是k=(y2-y1)/(x2-x1). ###输入 判断次数和2条线段的x1、y1、x2、y2 ###输出 是否相交 ###样例输入 3 1 5 2 9 1 3 2 4 5 6 7 8 5 7 7 7 2 5 1 0 9 4 2 9 ###样例输出 disjointdisjoint intersectintersect disjoint ``` ------------ 对于这道题,我最开始的想法是转化成二元二次方程组来求解。 很明显这个方法并不好写。原因如下: 计算中出现了除法(斜率计算、定比分点),因此每次计算前都要判断除数是否为 0(或接近 0)。这很麻烦,严重干扰逻辑的表达。 浮点精度丢失带来的误差。人类计算时可以采用分数,但计算机不行。计算机在储存浮点数时会有精度丢失的现象。一旦算法的计算量大起来,误差会被急剧放大,影响结果准确性。 效率低下。浮点乘除会十分耗时,不适用于对实时性要求较高的生产环境(如 游戏)。 那么,如何解决这个问题呢? ##思路 对于“判断两条直线是否相交”这个问题,我们之所以能迅速而准确地进行判断,是因为“相交”与“不相交”这两个状态有着明显的不同点,即 斜率是否相等。 那么现在,为了判断两条线段是否相交,我们也要找出“相交”与“不相交”这两个状态的不同点。 首先,两条线断在 X 轴和 Y 轴上的投影都要有重叠部分。(证明很简单不用说了吧) 假设现在有两条线段 AB 和 CD,我们画出它们之间的三种关系:  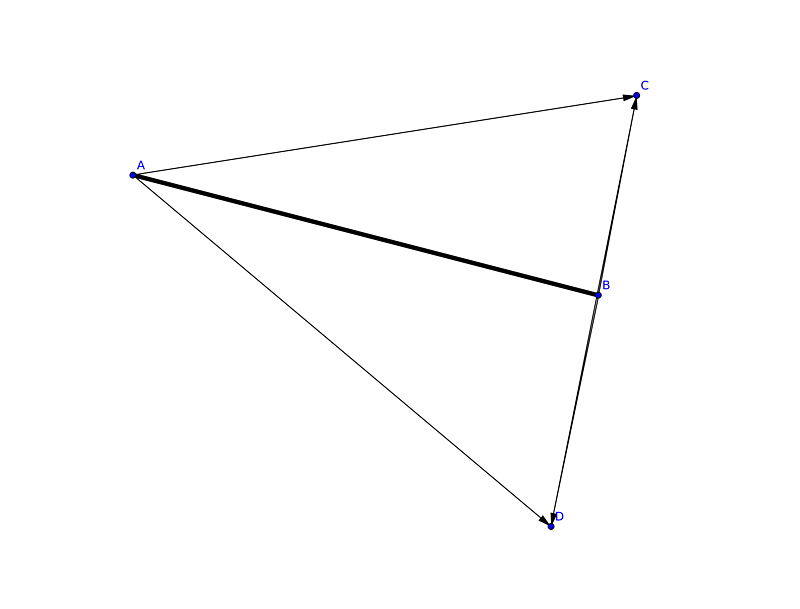 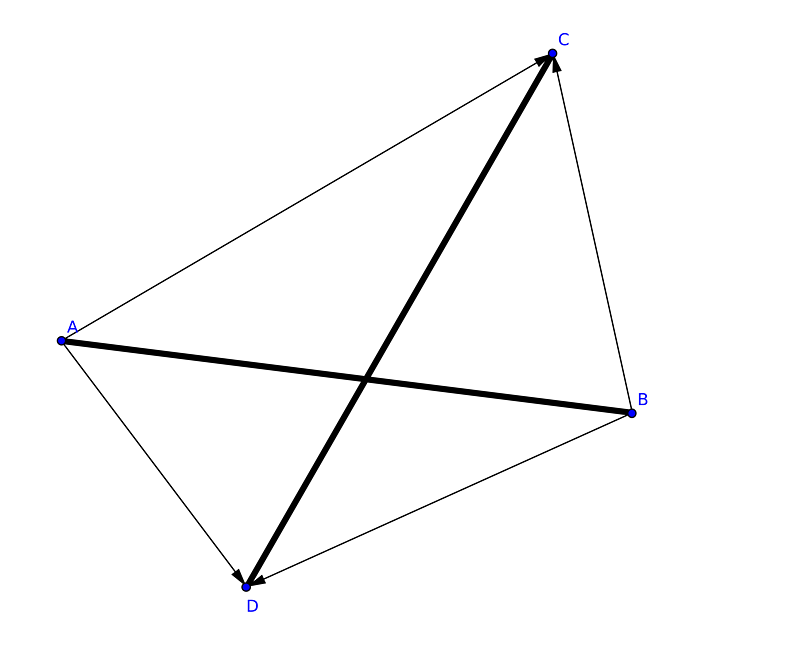 此时记两个向量的叉乘为 direct(**a**, **b**) ; 则有: 对于图一,direct(**AC**, **AD**) 和 direct(**BC**, **BD**) 都为顺时针,direct(**CA**, **CB**) 为逆时针,direct(**DA**, **DB**) 为顺时针。 对于图二,direct(**AC**, **AD**) 为顺时针,direct(BC, BD) 为任意方向,direct(**CA**, **CB**) 为逆时针,direct(**DA**, **DB**) 为顺时针。 对于图三,direct(**AC**, **AD**)、direct(**DA**, **DB**) 为顺时针,direct(**BC**, **BD**)、direct(**CA**, **CB**) 为逆时针。 所以,只需要向量 **AC** X **AD** 的方向和向量 **BC** X **BD** 相反或两者相乘为0,两条线段相交。 ##代码实现 ```cpp #include <iostream> #include <algorithm> using namespace std; //typedef pair<int,int> P struct node { int x, y; node() :x(0), y(0) { }; friend istream& operator >> (istream& in, node& a); }; istream& operator >> (istream& in, node& a)//重载流输入输出 { while (!(in >> a.x >> a.y)) return in; return in; } inline bool first_judge(node a, node b, node c, node d) {//判断两个线段的投影,投影相交才有可能有交点 if (max(a.x, b.x) < min(c.x, d.x) || min(a.x, b.x) > max(c.x, d.x)) return false; if (max(a.y, b.y) < min(c.y, d.y) || min(a.y, b.y) > max(c.y, d.y)) return false; return true; } inline int mul_cross(node a, node b, node c) {//计算向量ab, 向量ac 的叉乘 return (b.x - a.x)*(c.y - a.y) - (b.y - a.y)*(c.x - a.x); } inline bool IsCross(node a, node b, node c, node d) {//判断是否有交点 if (!first_judge(a, b, c, d)) return false; int tmp1 = mul_cross(a, c, d); int tmp2 = mul_cross(b, c, d); return tmp1 * tmp2 <= 0 ? true : false; } int main() { int t; cin >> t; while (t--) { node a, b, c, d; cin >> a >> b >> c >> d; IsCross(a, b, c, d) ? cout << "intersect" << endl : cout << "disjoint" << endl; } return 0; } ``` 参考资料: https://segmentfault.com/a/1190000004457595 最后修改:2019 年 04 月 03 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏