Loading... 学习数据结构与算法,就一定离不开对时间和空间的复杂度分析。我在这里总结一下我对复杂度分析的了解吧。 ##1. 什么是复杂度分析 数据结构与算法本身是用来解决“省”和“块”两个问题的。所以对于一个数据结构与算法来说,执行效率就是评判其好坏的一个重要的参考。那么如何估计一个算法的效率呢?这时候就需要复杂度分析了。它可以粗略的估计算法执行时间(或占用空间) 与数据规模的增长关系。 ##2. 为什么要进行复杂度分析 相对于直接跑一遍来进行精确测量,复杂度分析的部分优点如下: - 不依赖环境 - 成本低 - 易操作 同时,复杂度分析也可以让我们对代码执行有更深的理解,帮助我们写出更加优秀的代码,维护时也更加方便。 ##3. 如何进行复杂度分析 ###3.1 大O表示法 算法的执行时间与每行代码的执行次数成正比,用T(n) = O(f(n))表示,其中T(n)表示算法执行总时间,f(n)表示每行代码执行总次数,而n往往表示数据的规模。(有时候会有一些特例,比如基数排序。) ####特点 以时间复杂度为例,由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势,所以常量阶、低阶以及系数实际上对这种增长趋势不产决定性影响,所以在做时间复杂度分析时忽略这些项。 ###3.2 复杂度分析法则 ####1)单段代码看高频 在一些比较简单的代码中(比如说循环),我们就可以只看重复最多的那些代码。 ####2)多段代码取最大 比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。 ####3)嵌套代码求乘积 比如递归、多重循环等(自己写一段代码应该就懂了吧) ####4)多个规模求加法 比如代码中有两段循环,分别由两个参数控制循环的次数,那么这时就取二者复杂度相加。 ##4. 常见的复杂度级别 ###4.1 多项式阶 随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括, O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n^2)(平方阶)、O(n^3)(立方阶) ###4.2 非多项式阶 随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括, O(2^n)(指数阶)、O(n!)(阶乘阶) 给一张图来感受一下各个复杂度的效率: 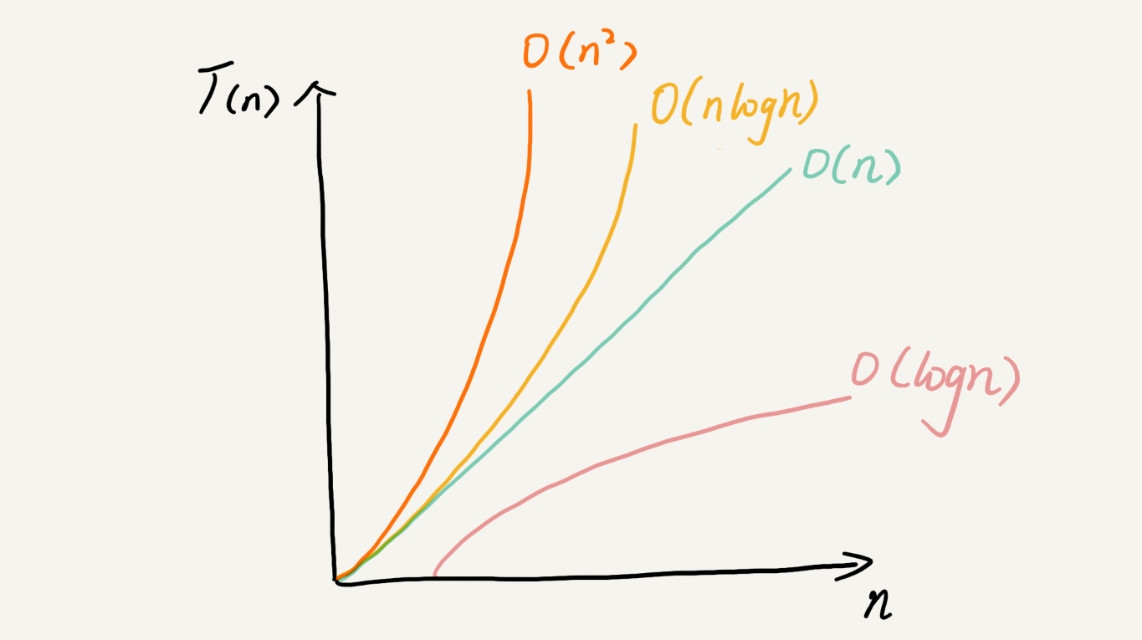 ##5. 随便写写 复杂度分析是一种思维方式,在写代码的时候多想想,这段代码会执行多少次?会不会有特殊情况?所谓熟能生巧,练多了自然就可以看一眼就估计出代码的复杂度了。 当然,我这里只写了基础复杂度分析。后面还有一些其他知识点。比如:最好情况时间复杂度(best case time complexity)、最坏情况时间复杂度(worst case time complexity)、平均情况时间复杂度(average case time complexity)、均摊时间复杂度(amortized time complexity)。这些后面有时间再写吧。XD 最后修改:2019 年 06 月 12 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏