Loading... 深度优先搜索(DFS, Depth-First Search)是搜索的手段之一。 ##1.算法思想 **深度优先搜索思想**:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。 @> 简单来讲,不撞南墙不回头 : ) ##2.算法特点 深度优先搜索是一个递归的过程。首先,选定一个出发点后进行遍历,如果有邻接的未被访问过的节点则继续前进。若不能继续前进,则回退一步再前进,若回退一步仍然不能前进,则连续回退至可以前进的位置为止。重复此过程,直到所有与选定点相通的所有顶点都被遍历。 深度优先搜索是递归过程,带有回退操作,因此需要使用栈存储访问的路径信息。当访问到的当前顶点没有可以前进的邻接顶点时,需要进行出栈操作,将当前位置回退至出栈元素位置。 @> 撞到南墙了那就只能回头咯 : ) ##3.算法过程 ###3.1 无向图的深度优先搜索 以下图所示的无向图为例来说明无向图的深度优先搜索遍历过程: 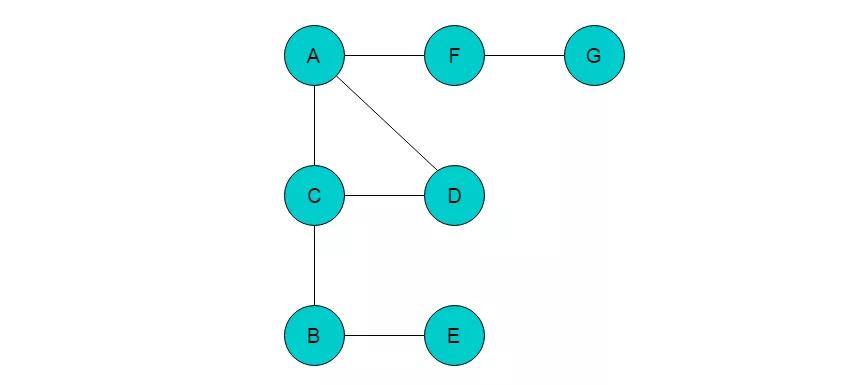 1. 首先选取顶点A为起始点,输出A顶点信息,且将A入栈,并标记A为已访问顶点。 2. A的邻接顶点有C、D、F,从中任意选取一个顶点前进。这里我们选取C顶点为前进位置顶点。输出C顶点信息,将C入栈,并标记C为已访问顶点。当前位置指向顶点C。 3. 顶点C的邻接顶点有A、D和B,此时A已经标记为已访问顶点,因此不能继续访问。从B或者D中选取一个顶点前进,这里我们选取B顶点为前进位置顶点。输出B顶点信息,将B入栈,标记B顶点为已访问顶点。当前位置指向顶点B。 4. 顶点B的邻接顶点只有C、E,C已被标记,不能继续访问,因此选取E为前进位置顶点,输出E顶点信息,将E入栈,标记E顶点,当前位置指向E。 5. 顶点E的邻接顶点均已被标记,此时无法继续前进,则需要进行回退。将当前位置回退至顶点B,回退的同时将E出栈。 6. 顶点B的邻接顶点也均被标记,需要继续回退,当前位置回退至C,回退同时将B出栈。 7. 顶点C可以前进的顶点位置为D,则输出D顶点信息,将D入栈,并标记D顶点。当前位置指向顶点D。 8. 顶点D没有前进的顶点位置,因此需要回退操作。将当前位置回退至顶点C,回退同时将D出栈。 9. 顶点C没有前进的顶点位置,继续回退,将当前位置回退至顶点A,回退同时将C出栈。 10. 顶点A前进的顶点位置为F,输出F顶点信息,将F入栈,并标记F。将当前位置指向顶点F。 11. 顶点F的前进顶点位置为G,输出G顶点信息,将G入栈,并标记G。将当前位置指向顶点G。 12. 顶点G没有前进顶点位置,回退至F。当前位置指向F,回退同时将G出栈。 13. 顶点F没有前进顶点位置,回退至A,当前位置指向A,回退同时将F出栈。 14. 顶点A没有前进顶点位置,继续回退,栈为空,则以A为起始的遍历结束。若图中仍有未被访问的顶点,则选取未访问的顶点为起始点,继续执行此过程。直至所有顶点均被访问。 15. 采用深度优先搜索遍历顺序为A->C->B->E->D->F->G。 ###3.2 有向图的深度优先搜索 以下图所示的有向图为例来说明有向图深度优先搜索遍历过程: 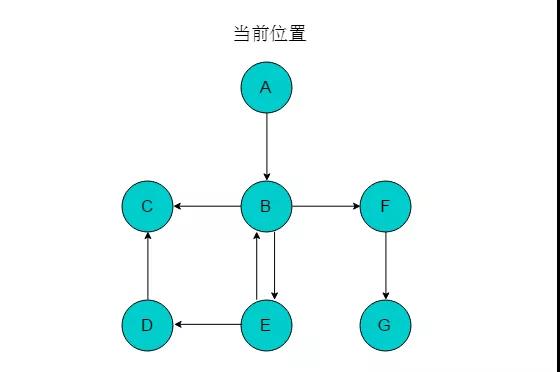 1. 以顶点A为起始点,输出A,将A入栈,并标记A。当前位置指向A。 2. 以A为尾的边只有1条,且边的头为顶点B,则前进位置为顶点B,输出B,将B入栈,标记B。当前位置指向B。 3. 顶点B可以前进的位置有C与F,选取F为前进位置,输出F,将F入栈,并标记F。当前位置指向F。 4. 顶点F的前进位置为G,输出G,将G入栈,并标记G。当前位置指向G。 5. 顶点G没有可以前进的位置,则回退至F,将F出栈。当前位置指向F。 6. 顶点F没有可以前进的位置,继续回退至B,将F出栈。当前位置指向B。 7. 顶点B可以前进位置为C和E,选取E,输出E,将E入栈,并标记E。当前位置指向E。 8. 顶点E的前进位置为D,输出D,将D入栈,并标记D。当前位置指向D。 9. 顶点D的前进位置为C,输出C,将C入栈,并标记C。当前位置指向C。 10. 顶点C没有前进位置,进行回退至D,回退同时将C出栈。 11. 继续执行此过程,直至栈为空,以A为起始点的遍历过程结束。若图中仍有未被访问的顶点,则选取未访问的顶点为起始点,继续执行此过程。直至所有顶点均被访问。 ##4.经典例题 这里就先放上一道洛谷的 N 皇后题目吧。 <button class=" btn m-b-xs btn-primary btn-addon" onclick="window.open('https://www.luogu.org/problemnew/show/P1219','_blank')"><i class="glyphicon glyphicon-hand-right"></i>题目戳我!</button> 再放一个我好久之前写的AC代码吧。(写的不好轻喷(o>ω<o) ) ```cpp #include <iostream> #include <vector> #include <string> #include <algorithm> #include <cstdlib> using namespace std; vector<vector<int> > result;//用来记录结果 vector<int> pos;//存放当前结果 int cnt = 0; bool check(int key, int value); void DFS(int begin, int end); int main() { int n; while (cin >> n) { result.clear(); cnt = 0; pos.resize(n+1);//分配 n 个空间来判断 DFS(1, n);//第一个空间是不用的 for (int i = 0; i < 3; i++) { for (int j = 1; j <= n; j++) { cout << result[i][j]; if (j != n) cout << " "; } cout << endl; } cout << cnt << endl; } } void DFS(int begin,int end) { if (begin > end)//所有位置都确定了 { if (cnt < 3) result.push_back(pos); cnt++; return; } for (int i = 1; i <= end; i++) {//循环 end 次来确定所有皇后的位置 if (check(begin, i)) {//如果该皇后可以放在位置 i 上 pos[begin] = i;//第 begin 个皇后就在位置 i 上 DFS(begin + 1, end);//继续搜索 } } return; } bool check(int key,int value) {//每一个皇后的八个方向都不能有皇后,所以需要这个check函数判断是否符合标准 for (int i = 1; i < key; i++) { if (pos[i] == value || abs(pos[i] - value) == abs(i - key)) return false; } return true; } ``` 再贴一份一位大佬写的位运算解法(等我哪天理解了再考虑写个详细点的解释吧QAQ): ```cpp #include<cstdio> int upperlim,n,ans,tot,plan[15]; void dfs(int i,int c,int ld,int rd)//变量含义:第i行(只是用来记录方案,如果不输出方案,可以去掉),c是行影响,ld、rd分别是左右对角线 { if(c==upperlim)//很好理解,如果是一个可行解的话自然所有列上都有棋子,如果不是可行解,看下面 { if(++ans<=3) { for(int i=1;i<n;i++) printf("%d ",plan[i]); printf("%d\n",plan[n]); } return; } int mask=upperlim&~(ld|rd|c);//mask指的是留下来能用的位置,受到行、左右对角线的影响。用upperlim & 则是要舍掉高位上多出来的1 while(mask)//尽管是穷举位,但是不用判断,因为如果不可行的话mask上没有能放的位置,根本到达不了最终状态就退出,位运算解法天然剪枝的高效、简洁是别的解法永远也追不上的 { int p=mask&(-mask);//技巧,表示mask末尾的第一个1,也就是穷举能放的位置 mask-=p;// plan[i]=__builtin_ffs(p);//__builtin_ffs(p)指的是p的末尾第一个1的位置,竞赛能不能用我不知道,但是据说有人WinterCamp用了AC dfs(i+1,c|p,(ld|p)<<1,(rd|p)>>1);//状态转移,c|p是行上影响,ld:对角线上首先增加了p的影响很好理解,左移则是对角线向下一行的自然延伸,rd同理 } } //尽管注释很详细,但是还是自己敲2,3遍才能理解 int main() { scanf("%d",&n); upperlim=(1<<n)-1;//目标状态 ans=0; dfs(1,0,0,0); printf("%d\n",ans); return 0; } ``` //小吴师兄写的文章里还有个算法分析,等我把图完全弄懂后再补上吧。 参考文章: 《算法竞赛入门经典》 小小吴师兄的文章 最后修改:2019 年 04 月 06 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏