Loading... 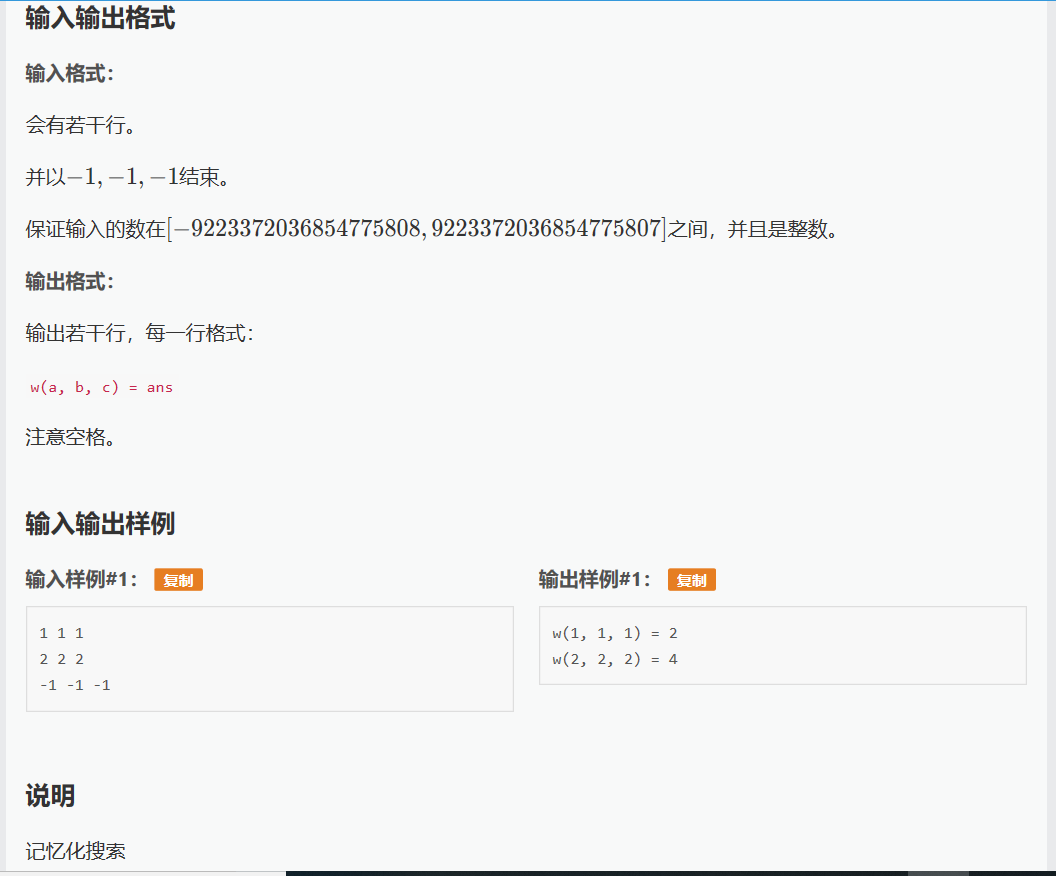 这个问题可以用简单的递归来解决,但其时间复杂度远大于4^n(oj每秒的算力是10^9级的)所以在1s的时限内不能只用递归来解决问题。 递归的时间复杂度之所以如此之高,是因为在递归过程中充满了重复计算,下图很好的体现了递归的特点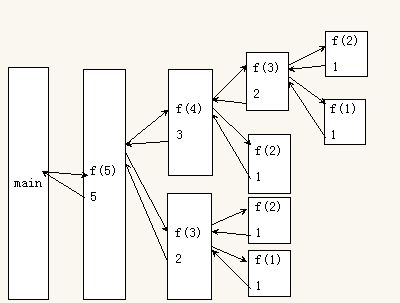 所以为什么我们要做这么多的无用功呢? 如果我能记忆每次递归的值,需要时进行调用,那就大大减少了时间复杂度。比如我令a[3]=f(3),a[4]=f(4),那么f(5)=a[3]+a[4],再令a[5]=f(5),那么f(6)=a[5]+a[4]就可以消除重复计算,大大缩短时间。 可以看到我们用少量的空间换取了大量的时间,这就是记忆化搜索的好处,代码如下: #include<stdio.h> int x[21][21][21]; void pai() { int i,j,k; for(i=0;i<21;i++) { for(j=0;j<21;j++) { for(k=0;k<21;k++) x[i][j][k]=10000; } } for(i=0;i<21;i++) { for(j=0;j<21;j++) { x[0][i][j]=1; x[i][0][j]=1; x[i][j][0]=1; } } } int w(long long int a,long long int b,long long int c); int main() { long long int a,b,c; pai(); while(scanf("%lld%lld%lld",&a,&b,&c)!=EOF) { if(a==-1&&b==-1&&c==-1) break; else { printf("w(%lld, %lld, %lld)=%d\n",a,b,c,w(a,b,c)); } } } int w(long long int a,long long int b,long long int c) { if(a<=0||b<=0||c<=0) return x[0][0][0]; else if(a>20||b>20||c>20) { a=b=c=20; x[a][b][c]=w(a,b,c); return w(a,b,c); } else if(a<b&&b<c) { if(x[a][b][c]==10000) { x[a][b][c]=w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c); } return x[a][b][c]; } else { if(x[a][b][c]==10000) { x[a][b][c]=w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1); } return x[a][b][c]; } }` 这个题目是一个星期前碰到的就随便写了写,后来想想这个代码有好多可优化的地方,但一直没去做(没错,就是懒(:з」∠)),像数组的初始化呀,递归返回值啊都有小问题。我本意是想通过这个题目拓展同学思路,所以请dalao不要吐槽我的代码质量啦= ̄ω ̄=  最后修改:2018 年 12 月 06 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏