Loading... 在所有的字符串匹配算法中,效率最高的应该是 BM 算法。但其中最有名的算法应该就是 KMP 算法了。很多时候我们提到字符串匹配,第一个想到的就是 KMP 算法。 那么 KMP 算法有什么奇妙的思想呢?本篇文章就来讨论一下 KMP 算法的原理和实现吧。 ## KMP 算法原理 KMP 算法全称 Knuth-Morris-Pratt 字符串查找算法, 由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表,故取这3人的姓氏命名此算法。 在具体讨论 KMP 算法的原理之前,我们先了解两个概念: **好前缀**和**坏字符**。 在模式串和主串匹配的时候,我们将不能匹配的那个字符叫做**坏字符**,已经匹配的字符串叫做**好前缀**。 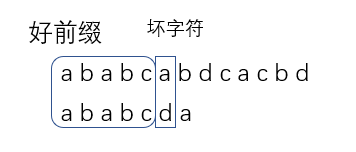 遇到坏字符的话,我们就需要将模式串向后滑动。在这个过程中,如果模式串与好前缀有重合,那么前几个字符的比较就相当于我们拿好前缀的后缀子串和模式串的前缀子串进行对比: 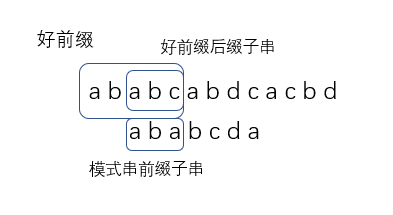 既然如此,我们是不是可以找到一些规律,让这个过程更加的高效呢? KMP 算法就是在寻找这样一种规律: 在模式串和主串匹配的过程中,如果遇到坏字符,如何根据已匹配的前缀向后滑动最多的位数? 我们只需要在好前缀的后缀子串中查找最长可与好前缀的前缀子串匹配的即可。假设最长的可匹配前缀子串{v}的长度为 k,坏字符的位置为 j,那么最大的滑动位数就是 j - k。也就是说,我们每次遇到坏字符的时候,就可以将模式串的位置更新为 k,再继续匹配。 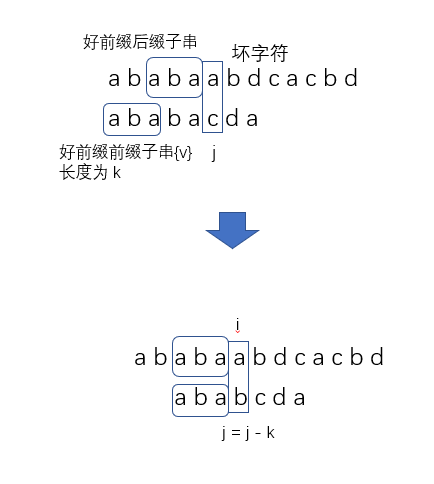 可以看到,我们滑动的位数只和模式串有关。那么我们是不是可以通过一些预处理,将不同最长可匹配前缀的位移记录下来,匹配的时候直接滑动呢?这样的话效率就可以提升许多了。 我们将这个预处理的数组叫做 **next 数组**。有些书中也给它取了个名字,叫做**失效函数(failure function)**。这个数组的下标就是好前缀的长度,里面的值储存的是模式串中每个前缀子串的最长可匹配子串的结尾下标。这个有点不好理解,我们看个例子: > 模式串: a b a b c a | 模式串前缀子串(好前缀候选) | 前缀字符串结尾下标 | 最长可匹配前缀子串结尾下标 | next值 | | -------------------------- | ------------------ | -------------------------- | ------------ | | a | 0 | -1 | next[0] = -1 | | ab | 1 | -1 | next[1] = -1 | | aba | 2 | 0 | next[2] = 0 | | abab | 3 | 1 | next[3] = 1 | | ababc | 4 | -1 | next[4] = -1 | 有了这个 next 数组后,KMP 算法就很好实现了。我们先假设 next 数组已经求出来了,将 KMP 的框架实现出来: ```cpp int KMP::find(const string& main_string) { int match = 0; // 好前缀的长度 for (auto i = 0; i < main_string.length(); i++) { while (match > 0 && main_string[i] != ptrn[match]) match = next[match - 1] + 1; if (main_string[i] == ptrn[match]) match++; // 找到匹配的字符串 if (match == ptrn.length()) return i - match + 1; } return -1; } ``` ## 失效函数的计算方法 前面已经写好了 KMP 算法的框架,那么剩下的问题就是这个 next 数组是怎么计算出来的了。 最简单的方法当然是暴力搜索所有子串,看看有没有和前缀相同的子串。但是这样肯定会影响 KMP 算法的执行效率。那有没有更好的方法呢? KMP 使用的方法非常巧妙,用到了一些动态规划的思想。下面我们就来看看它是怎么实现高效构建 next 数组的。 我们假设模式串为 ptrn。如果说 next[i - 1] = k - 1,也就是说子串 ptrn(0, k-1) 是 ptrn(0, i-1) 的最长可匹配前缀子串。然后我们看 ptrn[i] 和 ptrn[k]。如果他们两个相等的话,那么毫无疑问 ptrn(0, k) 就是 ptrn(0, i) 的最长可匹配前缀子串。所以 next[i] = k。 那么如果 ptrn[i] 和 ptrn[k] 不相等呢?我们就不可以简单的通过 next[i - 1] 计算出 next[i] 了。这个时候该怎么办呢? 我们假设子串 ptrn(r, i) 为子串 ptrn(0, i) 的最长可匹配后缀子串,那么 ptrn(r, i-1) 一定是 ptrn(0, i-1) 的可匹配后缀子串,但不一定是最长的。所以如果 ptrn[i] != ptrn[k] 的话,我们就可以去找 ptrn(0, i-1) 的次长可匹配后缀子串 ptrn(x, i-1) 对应的前缀子串 ptrn(0, i - 1 - x)。如果 ptrn[i - x] == ptrn[i],那么 ptrn(x, i) 就是 ptrn(0, i) 的最长后缀子串。 现在的问题就是如何找到这个次长可匹配后缀子串了。通过上面的分析,我们很容易知道: 次长可匹配后缀子串一定是包含于最长可匹配后缀子串中的。而最长可匹配后缀子串 ptrn(r, i) 又对应最长可匹配前缀子串 ptrn(0, y)。所以这个问题就转化为求子串 ptrn(0, y) 的最长后缀子串了。 按照这个思路,我们可以遍历 ptrn(0, i-1) 的所有可匹配后缀子串,直到找到一个可匹配的后缀子串 ptrn(y, i-1),它对应的前缀子串的下一个字符和 ptrn[i] 相同。此时 ptrn(y, i) 就是子串 ptrn(0, i) 的最长可匹配后缀子串。 这个失效函数是整个 KMP 算法中最难的一部分了。不理解的话可以动手画一下,加深对 next 数组的理解。这里给出我写的代码: ```cpp void KMP::generate_next() { next[0] = -1; int k = -1; // 最长可匹配前缀子串的结束下标 for (auto i = 1; i < ptrn.length(); i++) { // 寻找次长可匹配后缀子串 while (k != -1 && ptrn[k + 1] != ptrn[i]) k = next[k]; if (ptrn[k + 1] == ptrn[i]) k++; next[i] = k; } } ``` ## KMP算法 C++ 实现 > KMP.h ```cpp #pragma once #include <string> #include <vector> using std::string; using std::vector; class KMP { private: string ptrn; vector<int> next; void generate_next(); public: KMP(); explicit KMP(const string& p); ~KMP(); bool set_pattern(const string& p); int find(const string& main_string); }; ``` > KMP.cpp ```cpp #include "KMP.h" void KMP::generate_next() { next[0] = -1; int k = -1; // 最长可匹配前缀子串的结束下标 for (auto i = 1; i < ptrn.length(); i++) { // 寻找次长可匹配后缀子串 while (k != -1 && ptrn[k + 1] != ptrn[i]) k = next[k]; if (ptrn[k + 1] == ptrn[i]) k++; next[i] = k; } } KMP::KMP() = default; KMP::KMP(const string& p) { set_pattern(p); } KMP::~KMP() = default; bool KMP::set_pattern(const string& p) { ptrn = p; next.resize(ptrn.length()); generate_next(); return true; } int KMP::find(const string& main_string) { int match = 0; // 好前缀的长度 for (auto i = 0; i < main_string.length(); i++) { while (match > 0 && main_string[i] != ptrn[match]) match = next[match - 1] + 1; if (main_string[i] == ptrn[match]) match++; // 找到匹配的字符串 if (match == ptrn.length()) return i - match + 1; } return -1; } ``` > 测试代码 ```cpp #include <iostream> #include <chrono> #include "KMP.h" using namespace std; using namespace chrono; int main() { string a, b; while (cin >> a >> b) { auto begin = system_clock::now(); KMP kmp(b); int pos = kmp.find(a); auto end = system_clock::now(); auto duration = duration_cast<microseconds>(end - begin); cout << "查找结果为: " << pos << endl; cout << "一共花费了: " << double(duration.count()) * \ microseconds::period::num / microseconds::period::den \ << "秒" << endl; } return 0; } ``` 最后修改:2019 年 10 月 17 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏