Loading... 二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。 在二叉树的遍历中存在三种较为常用的遍历方式:前序遍历、中序遍历、后序遍历。(从上学期一直拖到现在才去了解) 我参考了小吴师兄的[一文弄懂二叉树的三种遍历](https://cxyxiaowu.com/articles/2019/04/04/1554345077929.html) ##准备 在了解二叉树的三序遍历之前,先来看一下这"三序"是什么。 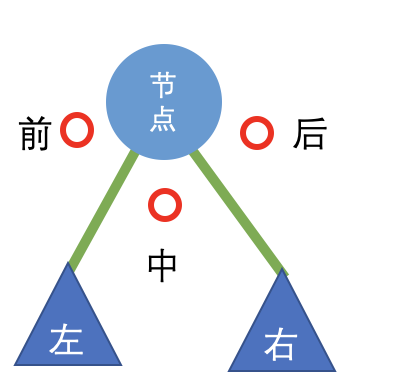 "前" 即为左节点 "中" 即为当前节点 "后" 即为右节点 这里的三个遍历就以我前面写的[二叉搜索树](https://blog.domineto.top/2019/04/07/BST.html)为例吧。 ##前序遍历 使用递归方式实现前序遍历的具体过程为: - 先访问根节点 - 再序遍历左子树 - 最后序遍历右子树 ###代码实现 ```cpp /***************************************************************** Function:preorderTraversal Description:前序遍历。 *****************************************************************/ void BST::__preorderTraversal(Node* node, vector<int> &res) { if (node) { res.push_back(node->value); __preorderTraversal(node->left, res); __preorderTraversal(node->right, res); } return; } vector<int> BST::preorderTraversal(Node* node) { vector<int> res; __preorderTraversal(node, res); return res; } ``` ##中序遍历 使用递归方式实现中序遍历的具体过程为: - 先中序遍历左子树 - 再访问根节点 - 最后中序遍历右子树 ###代码实现 ```cpp /***************************************************************** Function:inorderTraversal Description:中序遍历。 *****************************************************************/ void BST::__inorderTraversal(Node* node, vector<int> &res) { if (node) { __inorderTraversal(node->left, res); res.push_back(node->value); __inorderTraversal(node->right, res); } return; } vector<int> BST::inorderTraversal(Node* node) { vector<int> res; __inorderTraversal(node, res); return res; } ``` ##后序遍历 使用递归方式实现后序遍历的具体过程为: - 先后序遍历左子树 - 再后序遍历右子树 - 最后访问根节点 ###代码实现 ```cpp /***************************************************************** Function:postorderTraversal Description:后序遍历。 *****************************************************************/ void BST::__postorderTraversal(Node* node, vector<int> &res) { if (node) { __postorderTraversal(node->left, res); __postorderTraversal(node->right, res); res.push_back(node->value); } return; } vector<int> BST::postorderTraversal(Node* node) { vector<int> res; __postorderTraversal(node, res); return res; } ``` 最后修改:2019 年 04 月 11 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏